Éléments de cinétiques enzymatiques

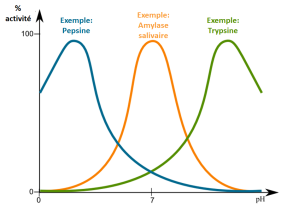
La figure ci-dessous montre la variation de l'activité d'une enzyme en fonction du pH.

Chaque enzyme possède un pH d'activité optimale, qui correspond à l'ionisation la plus adéquate des fonctions chimiques ionisables des acides aminés qui la composent.

Il faut noter que le pH d'activité optimale ne correspond pas toujours au pH de meilleure stabilité dans le temps de l'activité enzymatique.

L'effet de la température, lui, est double : d'une part, l'activité de l'enzyme suit la loi d'Arrhénius^[2] :

\({{V}_{\max }}={{V}_{0}}\times {{e}^{\frac{-{{E}_{a}}}{RT}}}\)

où : Ea = énergie d'activation.

donc a tendance à augmenter quand on augmente la température.

D'autre part, à partir d'une certaine température (qui dépend de l'enzyme ET de la composition du milieu), la structure de l'enzyme se trouve dénaturée (notamment avec la rupture des liaisons de faible énergie, dont les liaisons hydrogènes qui stabilisent la structure) et en perd progressivement son activité.

Le processus peut être réversible ou non. On peut en conséquence soit parler d'inactivation thermique soit de dénaturation thermique.

La combinaison de ces deux effets est représentée dans la figure ci-dessous.

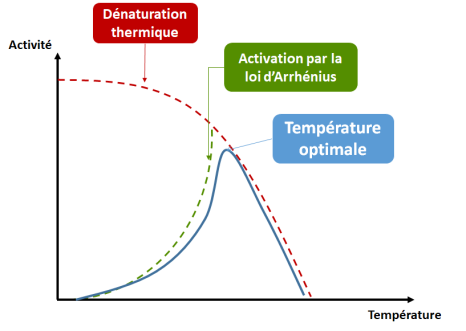
Lorsqu'une enzyme est utilisée longuement à une température où elle n'est pas stable et où elle perd progressivement de l'activité, on considère généralement que la dénaturation thermique suit une cinétique du premier ordre :

\({{V}_{\max }}={{V}_{\max 0}}\times {{e}^{-{{k}_{d}}\times t}}\)

où : \({V}_{\max 0}\) est la vitesse maximale initiale de l'enzyme (initiale = avant incubation à la température choisie) :

\({V}_{\max}\) est la vitesse maximale au bout d'un temps d'incubation t à la température choisie.

\({k}_{d}\) est la constante de dénaturation ou d'inactivation ([T]^-1).

La vidéo ci-dessous explicite l'influence de la température et du pH sur l'activité des enzymes :

Lorsqu'une enzyme est placée dans ses conditions physico-chimiques constantes (température, pH, force ionique), la vitesse initiale de la réaction qu'elle catalyse est proportionnelle à la quantité d'enzyme (à condition qu'il n'y ait pas de limitation par la concentration de substrat), comme le montre les deux figures ci-dessous :

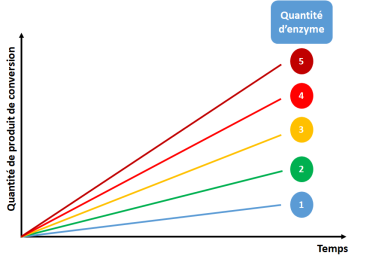
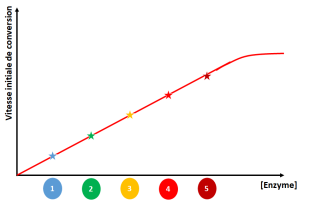
On constate qu'au-delà d'une certaine concentration, la vitesse initiale de la réaction n'augmente plus. Ceci s'explique par le fait que les enzymes ne se retrouvent plus en excès de substrat.

Toute utilisation d'une enzyme commence donc par l'établissement de cette zone de linéarité de la relation entre concentration d'enzyme et vitesse réactionnelle.\[\]

En choisissant une concentration d'enzyme dans la zone de linéarité présentée ci-dessus et en faisant varier la concentration initiale de substrat, on constate bien que la vitesse initiale de réaction augmente avec la concentration de substrat, jusqu'à atteindre, là aussi, un plateau. C'est ce qui est représenté par la figure ci-dessous. La valeur de vitesse maximale (V_max) est obtenue par l'asymptote.

V_max = Vitesse maximale de l'enzyme ;

K_M = constante d'affinité de l'enzyme pour son substrat.

L'allure de cette courbe vous rappelle probablement l'allure d'une isotherme de sorption qui obéit à un modèle de Langmuir (sorption sur charbon actif par exemple).

En 1913 Michaelis (biochimiste allemand) et Menten (médecin canadienne) proposent un modèle de cinétique enzymatique basé sur le même principe que ce que Langmuir publiera en 1921 sur la sorption. L'hypothèse de travail est commune : la cinétique est contrôlée (limitée) par la phase d'adsorption du substrat sur le site actif de l'enzyme. La réaction elle-même est beaucoup plus rapide donc pas limitante. L'équation de Michaelis-Menten est considérée comme un formalisme simplifié de l'équation de Langmuir.

Comme décrit plus haut, la réaction se fait en deux étapes : adsorption du substrat sur le site actif, puis sa transformation en produit. L'Interprétation de Michaelis-Menten se décompose donc en deux étapes :

\(\text{E+S}\overset{{{k}_{1}}}{\mathop{\underset{{{k}_{-1}}}{\mathop{\rightleftarrows }}\,}}\,\text{E-S}\)

\(E-S\overset{{{k}_{2}}}{\mathop{\to }}\,E+P\)

Si on écrit un bilan matière sur le substrat dans ce système, la variation de la quantité de substrat au cours du temps (c'est-à-dire la vitesse de la réaction, r) est égale à : \(\frac{d\left[ S \right]}{dt}=-r={{k}_{-1}}\left[ E-S \right]-{{k}_{1}}\left[ E \right]\left[ S \right]\)

Dans ce système, l'enzyme existe sous deux formes : libre et complexée avec le substrat : \(\left[ E-S \right]+\left[ E \right]={{\left[ E \right]}_{0}}\)

Par ailleurs, le bilan sur le complexe E-S peut donc être écrit comme suit : \(\frac{d\left[ E-S \right]}{dt}={{k}_{1}}\left[ S \right]\left[ E \right]-\left( {{k}_{-1}}+{{k}_{2}} \right)\left[ E-S \right]\)

Si en plus, on émet l'hypothèse de quasi-stationnarité, c'est-à-dire qu'à chaque instant, la quantité de complexes E-S qui se défait est compensée par autant de nouveaux complexes E-S qui se forment, alors \(\frac{d\left[ E-S \right]}{dt}=0\)

D'où la ré-écriture ci-dessous du bilan, dont la démonstration est disponible en Annexe :

K_M est appelée constante de Michaelis (vous remarquerez que l'histoire est souvent peu reconnaissante pour les femmes : la Dr Maud Menten a disparu de l'appellation). Cette constante K_M, si vous regardez la figure ci-dessus (dit "courbe de Michaelis - Menten"), est la concentration de substrat pour laquelle la vitesse de réaction vaut la moitié de la vitesse maximale. C'est une constante d'affinité de l'enzyme pour le substrat. Plus sa valeur est faible, plus l'affinité est élevée (c'est-à-dire que l'enzyme présente des vitesses élevées même pour des concentrations de S faibles).

\[\]

Comme indiqué plus haut, il est difficile d'obtenir précisément la valeur de Vmax en se basant sur l'asymptote de la courbe précédente. Communément, c'est une courbe en double inverse qui est utilisée : \(\frac{1}{V}=f\left( \frac{1}{\left[ S \right]} \right)\)

En effet : \(V=\frac{{{V}_{\max }}\left[ S \right]}{{{K}_{M}}+\left[ S \right]}\)

Donc : \(\frac{1}{V}=\frac{{{K}_{M}}+\left[ S \right]}{{{V}_{\max }}\left[ S \right]}\)

Donc : \(\frac{1}{V}=\frac{{{K}_{M}}}{{{V}_{\max }}}\times \frac{1}{\left[ S \right]}+\frac{1}{{{V}_{\max }}}\)

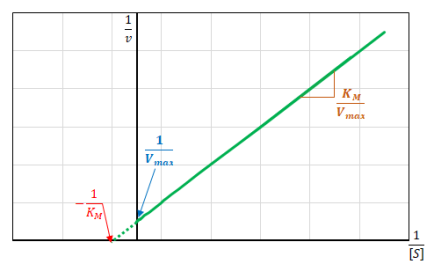
On voit donc que \(\frac{1}{V}=f\left( \frac{1}{\left[ S \right]} \right)\) donne une droite avec une ordonnée à l'origine égale à 1/V_max et qui coupe l'axe des abscisses à une valeur -1/K_M comme le montre la figure ci-dessous. C'est la représentation de Lineweaver-Burk.

La vidéo ci-dessous récapitule les éléments de cinétique enzymatique homogène :