Les réacteurs continus parfaitement agités
Principes généraux de dimensionnement des réacteurs enzymatiques continus
On considère un réacteur enzymatique, parfaitement mélangé, en fonctionnement continu : une alimentation continue en substrat est appliquée avec un débit volumique Q, avec une solution de concentration élevée notée [S]0. On applique également une sortie au même débit, de manière à maintenir constant le volume du réacteur.
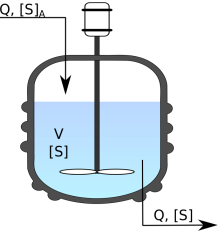
Le réacteur est supposé fonctionner à l'état stationnaire, c'est-à-dire qu'à tout instant, la concentration résiduelle de substrat est constante et notée [S]. En réalité, cette hypothèse n'est vraie qu'après un temps de démarrage dont on peut calculer la durée (voir cours de Génie de la réaction ou les cours précédents d'Introduction au génie des bioprocédés).
On ajoute dans ce réacteur une enzyme qui convertit le substrat S, en un produit P. On considère la concentration d'enzyme comme constante tout au long de la réaction.
La vitesse de transformation de S en P par l'enzyme est donnée par l'équation de Michaelis-Menten :
\(\frac{d\left[ S \right]}{dt}=-\frac{{{V}_{\max }}\left[ S \right]}{{{K}_{m}}+\left[ S \right]}\) (quantité de substrat converti par unité de volume et par unité de temps)
Dans le cas des réacteurs continus, on définit un taux de dilution, qui est le rapport du volume du réacteur sur le débit d'alimentation : τc=Q/V
On évalue ce taux de dilution appliqué en fonction des paramètres cinétiques de l'enzyme et du taux de conversion souhaité, avec l'équation suivante (où on évalue plutôt le temps passage, inverse du taux de dilution) :
\(\frac{V}{Q}=\frac{{{\left[ S \right]}_{0}}\theta }{{{V}_{\max }}}\left( \frac{{{K}_{m}}}{{{\left[ S \right]}_{0}}\left( 1-\theta \right)}+1 \right)\) |
|---|
Complément : Démonstration
Le bilan matière sur le réacteur enzymatique continu s'écrit : Entrée + transformation = sortie L'accumulation interne étant nulle puisque nous avons émis l'hypothèse du régime stationnaire. \(Q\times {{\left[ S \right]}_{0}}+r\times V=Q\times \left[ S \right]\) où r = vitesse de la réaction = \(\frac{d\left[ S \right]}{dt}\) Donc \(Q\times {{\left[ S \right]}_{0}}-Q\times \left[ S \right]=-r\times V\) Donc \(Q\times {{\left[ S \right]}_{0}}-Q\times \left[ S \right]=\frac{{{V}_{max}}\times \left[ S \right]}{{{K}_{M}}+\left[ S \right]}\times V\) Donc \(\left( {{\left[ S \right]}_{0}}-\left[ S \right] \right)=\frac{{{V}_{max}}\times \left[ S \right]}{{{K}_{M}}+\left[ S \right]}\times \frac{V}{Q}\) Donc \(\frac{{{K}_{M}}+\left[ S \right]}{{{V}_{max}}\times \left[ S \right]}\times \left( {{\left[ S \right]}_{0}}-\left[ S \right] \right)=\frac{V}{Q}\) Donc \(\frac{V}{Q}=\left( \frac{{{K}_{M}}}{\left[ S \right]}+1 \right)\times \frac{{{\left[ S \right]}_{0}}-\left[ S \right]}{{{V}_{max}}}\) Or : \({{\left[ S \right]}_{0}}-\left[ S \right]=\theta \times {{\left[ S \right]}_{0}}\) et \(\left[ S \right]={{\left[ S \right]}_{0}}\times \left( 1-\theta \right)\) Donc le bilan matière ci-dessus peut être ré-écrit comme suit : \(\frac{V}{Q}=\frac{{{\left[ S \right]}_{0}}\theta }{{{V}_{\max }}}\left( \frac{{{K}_{m}}}{{{\left[ S \right]}_{0}}\left( 1-\theta \right)}+1 \right)\) |
De la même manière que pour les réacteurs discontinus, nous avons démontré que le temps de réaction augmente avec le taux de conversion souhaité, ici nous constatons que les temps de passage dans le réacteur augmentent avec le taux de conversion :
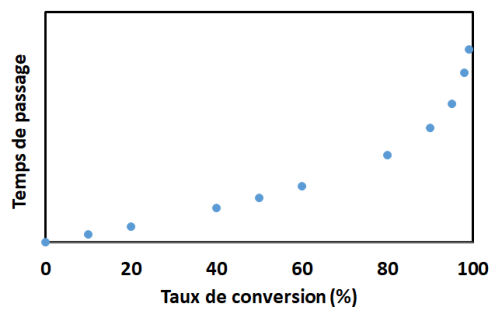
Il faut donc un temps de passage infini dans le réacteur pour convertir 100% du substrat.
Méthode :
Dans ce cas, pour un réacteur de volume connu, on peut donc décider du débit volumique, en fonction de l'objectif fixé en termes de taux de conversion. On peut également, à taux de dilution constant, faire varier la concentration de la solution d'alimentation, [S]0, pour ajuster le taux de conversion.
Les réacteurs continus parfaitement mélangés ont beau s'appeler ainsi, ils ne sont bien sûr pas parfaitement mélangés. Et vous pouvez, avec un traceur (un colorant ou un sel), vérifier l'existence d'une distribution des temps de séjour (notée DTS) donc d'une hétérogénéité des taux de conversion en leur sein (voir le Complément en fin de page).
Complément :
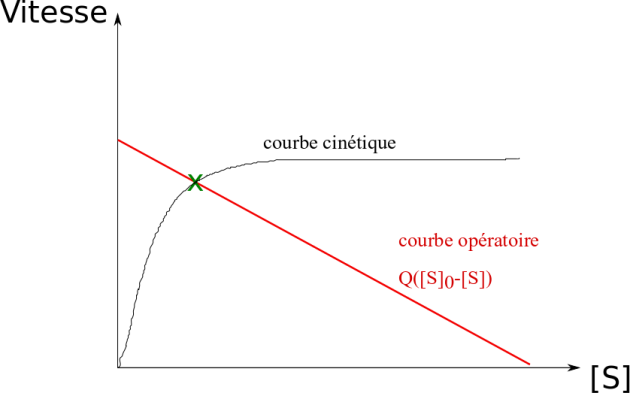
Pour déterminer le couple (concentration de substrat, vitesse de réaction) correspondant à l'état stationnaire, on soit résoudre le bilan matière précédent pour extraire l'expression de [S], soit procéder à une résolution graphique, comme indiqué dans la figure ci-dessous : on trace la courbe cinétique (Michaelienne dans les cas simples), et on y ajoute la droite opératoire \(Q\times {{\left[ S \right]}_{0}}-Q\times \left[ S \right]\). Le point d'intersection représente la condition de fonctionnement à l'état stationnaire (égalité des deux termes : opératoire et cinétique) :
Remarque :
Hypothèse sous-jacente dans ce qui précède (état stationnaire) : la quantité d'enzyme est constante dans le réacteur.
Or, nous avons précisé au début de ce paragraphe qu'il s'agissait d'un réacteur continu.
Plusieurs cas de figures sont possibles :
Alimentation continue en enzyme, avec le débit Q
Inconvénient : coût enzymatique important.
Maintien de l'enzyme dans le réacteur : filtration membranaire à la sortie du réacteur
Immobilisation de l'enzyme dans un support solide (billes, gels).
Si aucune de ces solutions n'est appliquée, le réacteur n'a pas de fonctionnement en état stationnaire. Il subit un lessivage de l'enzyme au cours du temps, comme le montre la figure ci-dessous :
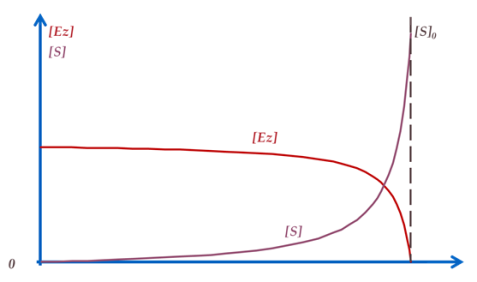
Dans ce cas, la concentration d'enzyme dans le réacteur diminue au cours du temps, donc la vitesse de réaction aussi. Il en résulte que la concentration de substrat non convertit devient de plus en plus élevée dans le réacteur, jusqu'à atteindre un simple passage du substrat sans conversion.
Le maintien de l'enzyme dans le réacteur est donc indispensable. Quelle que soit la solution technique envisagée à cette fin, il en résulte des limitations diffusionnelles (membrane de filtration, bille solide d'immobilisation de l'enzyme, etc) qui ne seront pas traitées dans le cadre de ce cours.
Méthode : Récapitulons
La vidéo ci-dessous récapitule les éléments de calcul pour un réacteur enzymatique continu. Si nous avons démontré ci-dessus l'influence du taux de conversion sur le temps de séjour, dans cette vidéo c'est une autre approche qui est conduite et qui va montrer l'influence du temps de séjour sur la concentration de sortie de S et donc sur le taux de conversion.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Réacteurs enzymatiques continus avec inhibition
Dans le cas d'une inhibition de la réaction enzymatique par son produit, les bilans matières s'écrivent de la même manière que précédemment, mais le dimensionnement du réacteur continu doit être adapté, en prenant en compte cette inhibition dans l'écriture du modèle cinétique (voir le cours sur les cinétiques enzymatiques, exemple d'une inhibition compétitive).
On peut distinguer deux cas de figure :
le cas d'une inhibition de la réaction enzymatique par le produit : dans ce cas, la concentration d'inhibiteur dans le réacteur peut être conséquente (si on vise une conversion maximale), ce qui rend l'utilisation d'une réacteur continu parfaitement mélangé inadaptée ;
le cas d'une inhibition de la réaction par le substrat : cette inhibition peut être minimisée en adaptant la concentration d'alimentation en substrat et le temps de passage, de manière à avoir une conversion maximale du substrat. Les concentrations résiduelles dans le réacteur continu parfaitement mélangée sont alors faibles et l'utilisation de ce mode opératoire reste envisageable.
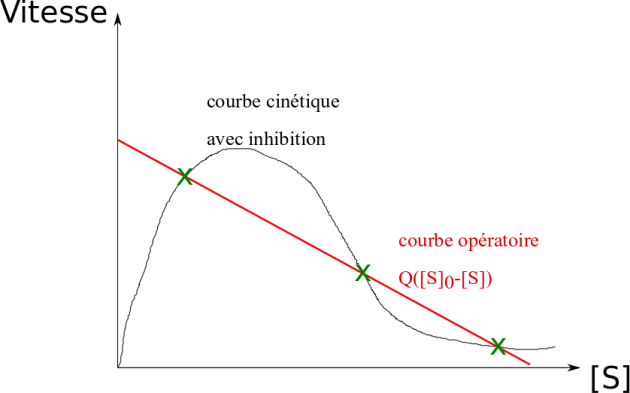
Dans ce dernier cas, la courbe de cinétique réactionnelle en fonction de [S] ressemble d'abord à une courbe Michaelienne pour les faibles concentrations de substrat, avant de décliner pour les concentrations croissantes.
Si on représente cette courbe cinétique, et qu'on représente sur le même graphique la courbe opératoire : \(Q\times {{\left[ S \right]}_{0}}-Q\times \left[ S \right]\) (figure ci-dessous), on observe que ces deux courbes se croisent en plusieurs points, qui correspondent à l'égalité donnée dans la démonstration ci-dessus : \(Q\times {{\left[ S \right]}_{0}}-Q\times \left[ S \right]=\frac{{{V}_{max}}\times \left[ S \right]}{{{K}_{M}}+\left[ S \right]}\times V\). Ces points d'intersection correspondent à ce qu'on appelle des états stationnaires multiples, qu'on identifie donc aisément par cette méthode graphique.
La vidéo ci-dessous récapitule le phénomène d'inhibition par le substrat dans les réacteurs enzymatiques continus. L'approche analytique et l'approche graphique (représentation de la droite opératoire) sont décrites dans cette vidéo.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Complément : Suite...
Pour ceux qui le souhaitent, une explication de la distribution des temps de séjour et de l'intérêt des réacteurs piston (paragraphe suivant) est présentée dans la vidéo suivante :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.