Quantification d’un procédé de production de levures à forte teneur en protéines
Fermentation en batch
Une souche de levure, possédant un taux de protéines intracellulaires de 50% est utilisée pour produire des protéines d’organismes unicellulaires, à destination de l’alimentation animale. Elle est caractérisée par un temps de doublement de 1h30 et un rendement de croissance sur sucres YX/S de 0,5 g/g. Elle suit une loi de Monod, caractérisée par une constante de limitation KS de 0,01 g/L.
Afin de produire des protéines d’organismes unicellulaires à grande échelle, un fermenteur de 30 m3 contenant 20 m3 de milieu de culture composé de 77 g/L de saccharose (Sm) et 11 g/L d'urée (Um) est inoculé par un pré-fermenteur inoculum de 2 m3 contenant 16,5 g/L de levures (Xi) et des concentrations négligeables en substrats résiduels.
Données : | § 1 g d'azote N correspond à 6,25 g de protéines § masse molaire azote moléculaire = 14 g (N) § masse molaire de l'urée = 60 g (N2COH4) |
Teneur protéines | P% | % | 50% |
Temps de génération | Tg | h | 1,5 |
Rendement de croissance | Yx/s | g/g | 0,5 |
Constante de saturation | Ks | g/L | 0,01 |
Masse molaire azote moléculaire | mmN | g/mol | 14 |
Masse molaire urée | mmU | g/mol | 60 |
Rapport protéines sur azote moléculaire |
| g/g | 6,25 |
Conc en biomasse inoculum | X0i | g/L | 16,5 |
Volume inoculum | Vi | m3 | 2,0 |
Conc en saccharose milieu | S0m | g/L | 77,0 |
Conc en urée milieu | U0m | g/L | 7,0 |
Volume milieu | Vm | m3 | 20,0 |
Temps entre 2 batchs | T | h | 6,0 |
Question
Déterminer le taux de croissance maximum (µM, en h-1) de la levure.
Solution
Le taux de croissance maximum est défini par \(µ_{max}=\frac{ln2}{t_g}\)
Donc \(µ_{max}=\frac{ln2}{1,5}=0,462\) h-1.
Question
Calculer les concentrations initiales en biomasse et en substrats carboné et azoté (en g/L).
Solution
La concentration initiale de substrat carboné s'écrit : \(S_0=S_{0m}\frac{V_m}{V_m+V_i}\)
Donc \(S_0=77\frac{20}{20+2}=70\) g/L.
De même, la concentration initiale en urée s'écrit : \(U_0=U_{0m}\frac{V_m}{V_m+V_i}\)
Donc \(U_0=7\frac{20}{20+2}=6,4\) g/L
Enfin, la concentration initiale de cellules s'écrit : \(X_0=X_{0i}\frac{V_i}{V_m+V_i}\)
Donc \(X_0=16,5\frac{2}{20+2}=1,5\) g/L
Question
Calculer les concentrations finales en biomasse et en substrat carboné (en g/L). Quelles hypothèses doit-on faire ?
Solution
On peut calculer la concentration finale de biomasse comme suit : \(X_f=X_0+S_0\times Y_{X/S}\) en supposant le substrat carboné limitant, donc Sf=0 g/L.
Donc \(X_f=1,5+70\times 0,5=36,5\) g/L
Question
Calculer le rendement de croissance sur l’urée (YX/U, en g/g) et la concentration finale en substrat azoté (en g/L).
Solution
Le rendement de croissance sur l'urée s'écrit \(Y_{X/U}=\frac{X_f-X_0}{U_0-U_f}\)
Pour pouvoir le calculer, il est donc nécessaire de déterminer la concentration finale d'urée. Cette dernière peut être déduite à partir de la quantité d'urée donc d'azote incorporée par les cellules au cours de la croissance. Or on sait que les cellules mises en culture possèdent un taux de protéines intracellulaires de 50%.
Donc \(\Delta Prot=\Delta X *\% P\)
Donc \(\Delta Prot = (36,5-1,5)*50\%=17,5\) g/L
On peut convertir cette variation en variation de quantité d'azote : \(\Delta N=\Delta Prot /6,25 =17,5/6,25=2,8\) g/L
Ceci permet de déduire la variation totale de quantité d'urée, sur la base de sa teneur en azote : \(\Delta U= \Delta N \frac{M(Uree)}{M(N_2)}\)
Donc \(\Delta U=2,8\times 60/(14*2)=6\) g/L
Ainsi, la concentration finale en urée est \(\)\(U_f=6,4-6=0,4\) g/L
Ceci permet de calculer enfin le rendement de croissance sur l'urée : \(Y_{X/U}=\frac{36,5-1,5}{6,4-0,4}=5,83\) g/g
Question
Calculer la durée de la phase de croissance exponentielle (tf, en h) et représenter l’évolution des concentrations en biomasse et en substrats en fonction du temps.
Solution
\(t_f=\frac{1}{µ_{max}}ln\frac{X_f}{X_0}\)
Donc \(t_f=\frac{1}{0,462}ln\frac{36,5}{1,5}=6,91\) h
Méthode :
Entre 0h et 6,91h, on a donc une croissance exponentielle, ce qui permet d'appliquer la loi de croissance : \(X=X=0e^{µ_{max}t}\)
On peut faire évoluer les concentrations de substrat progressivement, en les fixant à différentes valeurs décroissantes en partant de la valeur initiale de 70. Pour chaque \(\Delta S\) on peut calculer un \(\Delta X\) grâce au rendement de conversion\(Y_{X/S}\), ce qui permet ensuite de calculer la concentration d'urée correspondante, via le rendement \(Y_{X/N}\).
Enfin, le temps correspondant à chaque itération est calculé comme étant \(t=\frac{1}{µ_{max}ln\frac{X}{X_0}}\)
Le tracé des évolutions au cours du temps donne :
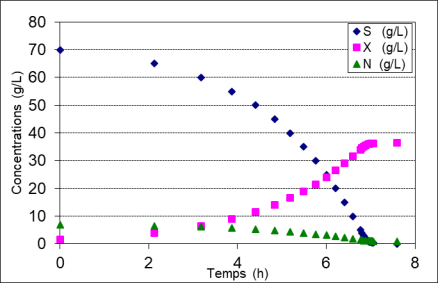
Question
Calculer, en fonction du temps, le taux de croissance réel de la souche si l’on prend en compte sa constante de saturation. Représenter la variation temporelle du taux de croissance.
Question
Quelle conséquence la prise en compte de la constante de saturation a-t-elle sur la durée de la fermentation. Calculer cette nouvelle durée.
Solution
La prise en compte de la phase de ralentissement permet de calculer les valeurs réelles du taux de croissance \(µ=µ_{max}\frac{S}{K_S+S}\) pour chaue concentration résiduelle S de substrat. Cela aboutit à un allongement de la durée de fermentation de 6,91 h à 7,6 h comme le montre le tableau suivant :
tps (h) | S (g/L) | X (g/L) | N (g/L) | µ Monod (h-1) |
0 | 70 | 1,5 | 7 | 0,462 |
2,12 | 65 | 4 | 6,57 | 0,462 |
3,17 | 60 | 6,5 | 6,14 | 0,462 |
3,88 | 55 | 9 | 5,71 | 0,462 |
4,41 | 50 | 11,5 | 5,29 | 0,462 |
4,83 | 45 | 14 | 4,86 | 0,462 |
5,19 | 40 | 16,5 | 4,43 | 0,462 |
5,50 | 35 | 19 | 4,00 | 0,462 |
5,76 | 30 | 21,5 | 3,57 | 0,462 |
6,00 | 25 | 24 | 3,14 | 0,462 |
6,22 | 20 | 26,5 | 2,71 | 0,462 |
6,41 | 15 | 29 | 2,29 | 0,462 |
6,60 | 10 | 31,5 | 1,86 | 0,462 |
6,77 | 5 | 34 | 1,43 | 0,461 |
6,80 | 4 | 34,5 | 1,34 | 0,461 |
6,84 | 3 | 35 | 1,26 | 0,461 |
6,88 | 2 | 35,5 | 1,17 | 0,460 |
6,95 | 1 | 36 | 1,09 | 0,458 |
6,97 | 0,8 | 36,1 | 1,07 | 0,456 |
7,00 | 0,6 | 36,2 | 1,05 | 0,455 |
7,03 | 0,5 | 36,25 | 1,04 | 0,453 |
7,07 | 0,4 | 36,3 | 1,03 | 0,451 |
7,59 | 0,1 | 36,45 | 1,01 | 0,420 |