Production d'une levure de boulangerie
1/ Production dans un réacteur discontinu parfaitement agité
L'étude cinétique en culture batch aéré de la production de levure de boulangerie Saccharomyces cerevisiae donne les résultats suivants :
Temps (h) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 14 | 16 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
[X] (g/L) | 0,20 | 0,21 | 0,25 | 0,33 | 0,42 | 0,55 | 0,70 | 0,82 | 0,90 | 0,92 | 0,95 | 1,15 | 1,35 | 1,60 | 1,65 |
[S] (g/L) | 5,00 | 4,80 | 4,60 | 4,00 | 3,40 | 2,60 | 1,50 | 0,50 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
[P] (g/L) | 0,00 | 0,00 | 0,10 | 0,20 | 0,35 | 0,50 | 0,75 | 0,90 | 1,05 | 1,00 | 0,95 | 0,70 | 0,40 | 0,10 | 0,00 |
On supposera qu'il n'y a aucune limitation de la croissance par l'oxygène.
Question
a- En traçant sur un même graphique les courbes donnant X, S et P en fonction du temps, deux phases de croissance ressortent. Commenter.
b- Déterminer ces phases calculer leurs durées respectives.
Solution
Le tracé des trois courbes donne :
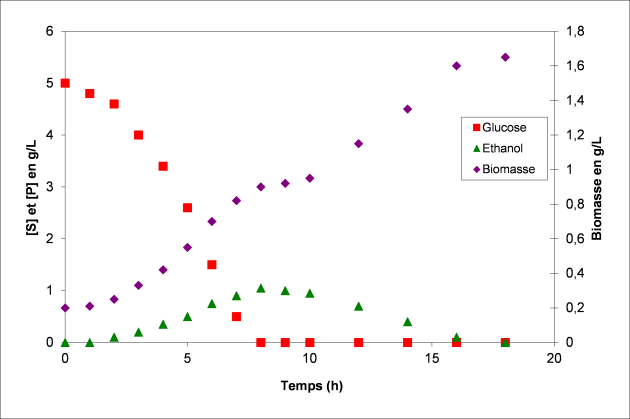
On constate deux phases de croissance des levures:
- La première de 0h à 8h, de croissance de la levure en consommant du glucose. On constate néanmoins pendant cette phase que le glucose n’est pas uniquement utilisé pour la croissance cellulaire mais qu’il est partiellement utilisé pour produire de l’éthanol, ce qui n’est pas l’objectif de l’opération. Ce dernier est de produire de la biomasse (cellules de levures).
- La deuxième phase de 8h à 18h, qui commence par une stagnation de la concentration de levures, due à l’épuisement de glucose. Au début de cette phase, les levures adaptent leur métabolisme à la seule source de carbone existante dans le milieu : l’éthanol. Une fois les enzymes nécessaires à l’oxydation de l’éthanol fabriquées, la croissance des levures redémarre, et est possible grâce à la consommation d’éthanol.
Il faut noter qu’aucun organisme vivant n’est capable de métaboliser de source de carbone en même temps. La source de carbone la plus commune, le glucose, est prioritairement métabolisée. C’est seulement une fois celle-ci épuisée que l’organisme vivant en métabolise une deuxième, puis une troisième, etc.
Dans chacune de ces phases, on distingue donc une période de latence et une période de croissance exponentielle, dont on peut déterminer la constante (µ, appelée vitesse spécifique de croissance). On peut déterminer sa valeur en traçant le ln de la concentration de levures en fonction du temps. On obtient une droite dont la pente est égale à µ.
Question
c- Calculer la vitesse spécifique de croissance sur glucose et sur éthanol.
Indice
Tracer la courbe de croissance semi-logarithmique
Solution
La courbe semi-logarithmique de croissance des levures permet de déterminer les vitesses spécifiques de croissance :
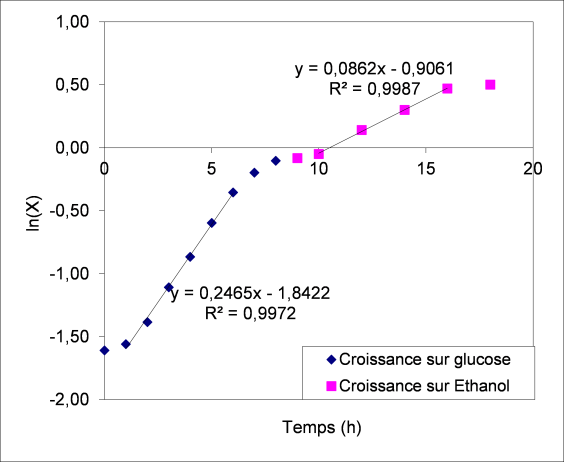
On obtient :
La vitesse spécifique de croissance de la levure sur glucose = 0,246 h-1
La vitesse spécifique de croissance de la levure sur éthanol = 0,086 h-1
Détermination des rendements de conversion
Question
d- Calculer les rendements de conversion du glucose en biomasse et du glucose en éthanol pendant la première phase de croissance.
Solution
1e phase (0-8h)
Les rendements de conversion du glucose en biomasse (YG/X) et en éthanol (YG/E) sont calculés comme suit :
\({{Y}_{X/S}}=\frac{0,9-0,2}{5-0}=14\%\)
\({{Y}_{P/S}}=\frac{1,05-0}{5-0}=21\%\)
Question
e- Calculer le rendement de conversion de l'éthanol en biomasse pendant la deuxième phase de croissance.
Solution
2e phase (8-18h)
Le rendement de conversion de l’éthanol en biomasse pendant la deuxième phase est calculé comme suit :
\({{Y}_{X/P}}=\frac{1,65-0,9}{1,05-0}=71\%\)
2/ Production dans un réacteur fed-batch
La production de la levure de boulangerie même dans un réacteur aéré s'accompagne d'une production d'éthanol en présence d'excès de source de carbone (ici glucose).
Pour minimiser cette production d'éthanol et améliorer la production de biomasse, il est nécessaire de ne pas dépasser un seuil critique de la concentration en glucose au cours de la croissance de la levure. Un bioréacteur en mode fed-batch est mis en œuvre dans ce but.
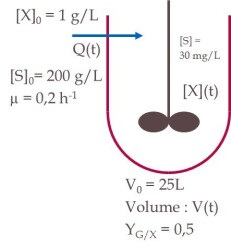
Pour Saccharomyces cerevisiae, la concentration optimale de glucose à 30 °C est de 30 mg/L. Dans ces conditions, la vitesse spécifique de croissance µ est de 0,2 h-1 et le rendement de conversion du glucose en biomasse est de 0,5.
Question
a- Comparer avec les résultats de la culture précédente en mode batch.
Solution
La vitesse spécifique de croissance est légèrement plus faible qu’en batch, mais il ne faut pas perdre de vue que la concentration de substrat est 167 fois plus faible.
Le rendement de conversion de G en X est meilleur, certainement parce que la production d'éthanol, inhibiteur de la croissance, est inexistante.
Mise en oeuvre :
On met donc en œuvre la production de Saccharomyces cerevisiae dans une cuve de fermentation alimentée en continu par un milieu contenant 200 g/L de glucose. Le débit de sortie est nul. Le fermenteur contient initialement 25 L de milieu de culture contenant 1 g/L de levure et 30 mg/L de glucose.
La concentration de glucose est maintenue constante pendant toute l'opération.
Question
b- Quelle sera la fonction « débit Q » à programmer pour maintenir la concentration de glucose à 30 mg/L pendant toute l'opération ?
Solution
Le bilan matière établi sur la quantité de levure s’écrit comme suit:
\(V\times \left[ X \right]={{V}_{t0}}\times {{\left[ X \right]}_{t0}}\times \exp \left( \mu \times t \right)\)
Le bilan matière établi sur la quantité de glucose s’écrit :
\(\frac{d}{dt}\left( V\times \left[ S \right] \right)=Q\times {{\left[ S \right]}_{0}}-V\times {{r'''}_{S}}\)
Or S=cste = 30 mg/L donc \(\left[ S \right]\times \frac{d}{dt}\left( V \right)=Q\times {{\left[ S \right]}_{0}}-V\times {{r'''}_{S}}\)
Par ailleurs : \(\begin{cases} & \frac{dV}{dt}=Q \\ & {{r'''}_{s}}={{r'''}_{x}}/{{Y}_{X/S}}\text{ et }{{r'''}_{x}}=\mu \times X \\ \end{cases}\)
donc \(Q\times \left( {{S}_{0}}-S \right)=\frac{V\times \mu \times X}{{{Y}_{X/S}}}\)
Dans le bilan matière sur la biomasse, le produit VX est remplacé par son expression d’après la dernière équation (et n’est pas dissocié car V et X sont des variables dépendantes l’une de l’autre).
D’où : \(\frac{Q\times \left( {{S}_{0}}-S \right)}{\mu }\times {{Y}_{X/S}}={{V}_{t0}}\times {{\left[ X \right]}_{t0}}\times \exp \left( \mu \times t \right)\)
Donc \(Q=\frac{\mu \times {{V}_{t0}}\times {{\left[ X \right]}_{t0}}\times \exp \left( \mu \times t \right)}{\left( {{S}_{0}}-S \right)\times {{Y}_{X/S}}}\)
Application numérique :
\(Q=0,05\times \exp \left( 0,2\times t \right)\) |
Le glucose n'étant jamais limitant, la production de levure s'arrête par manque de dioxygène (valeur critique : 1 mg/L)
Question
c- Calculer la vitesse maximale de transfert d'oxygène par unité de volume.
Données : kLa = 700 h-1 ; [O2]* = 14 mg/L
Indice
Il s’agit de considérer ici l'expression générale de transfert de matière aux interfaces en appliquant le modèle du film. Si vous ne parvenez pas à résoudre cette question, vous pouvez préalablement vous reporter au cours suivant, sur le transfert de matière gaz-liquide.
Solution
La vitesse maximale de transfert de l’oxygène de la phase gazeuse (bulles d’air) vers la phase liquide est conditionnée par les propriétés rhéologiques du milieu de culture et les conditions d’agitation \(\Rightarrow\) kLa, ainsi que par les propriétés de solubilité de l’oxygène, et du seuil critique en dessous duquel le métabolisme des levures risque d’être modifié.
\({{\left( \frac{d\left[ {{O}_{2}} \right]}{dt} \right)}_{\max }}={{k}_{L}}a\times \left( {{\left[ {{O}_{2}} \right]}^{*}}-{{\left[ {{O}_{2}} \right]}_{critique}} \right)\)
Application numérique:
\({{\left[ {{O}_{2}} \right]}^{*}}\)= 14 mg/L ; \({{\left[ {{O}_{2}} \right]}_{critique}}\)= 1 mg/L ; kLa = 700 h-1
Donc : \({{\left( \frac{d\left[ {{O}_{2}} \right]}{dt} \right)}_{\max }}=700\times \left( 0,014-0,001 \right)=9,1\text{ g}\text{.}{{\text{L}}^{\text{-1}}}\text{.}{{\text{h}}^{\text{-1}}}\)
Question
d- Calculer la vitesse maximale de production de levure par unité de volume. (YX/O = 0,85)
Solution
L’oxygène consommé sert essentiellement à la multiplication des levures. Il a donc, comme tous les substrats, un rendement de conversion en biomasse. On peut donc, à partir de ce rendement et de la vitesse maximale de transfert d’oxygène, calculer la vitesse maximale de production de levure, qu’il ne faut pas dépasser, sous peine d’avoir des levures en déficit d’oxygène, donc de métabolisme modifié.
\({{\left( \frac{d\left[ X \right]}{dt} \right)}_{\max }}={{\left( \frac{d\left[ {{O}_{2}} \right]}{dt} \right)}_{\max }}\times {{Y}_{X/{{O}_{2}}}}\)
\(\text{=}9,1\times 0,85\)
\(= 7,74 g/L/h\)
Question
e- Quelle est la concentration maximale de biomasse ?
Solution
A l’instant où la vitesse de production de levures atteint la valeur ci-dessus, la concentration de levure est alors égale à :\(X=\frac{\mu }{{{\left( \frac{d\left[ X \right]}{dt} \right)}_{\max }}}\)
X= 38,7 g/L
Quand cette concentration est atteinte, le transfert d’oxygène ce déroule une vitesse qui correspond à la vitesse de croissance de levures. Comme le transfert d’oxygène ne peut pas être opéré à une vitesse plus importante, il faut arrêter la culture à ce moment, afin d’éviter une prolongation non optimale du procédé (début de fermentation alcoolique = production d’éthanol, donc mauvaise rentabilisation du substrat glucose).
Question
f- La fermentation s'arrêtant au bout de 24 h, quel est alors le volume de milieu dans le fermenteur ?
Solution
\(Q=0,05\times \exp \left( 0,2\times t \right)=\frac{dV}{dt}\)
Donc \(dV=0,05\times \exp \left( 0,2\times t \right)\times dt\)
\(\int\limits_{{{V}_{0}}}^{{{V}_{f}}}{dV}=0,05\times \int{\exp \left( 0,2\times t \right)\times dt}\)
Donc \({{V}_{f}}-{{V}_{0}}=0,05\times \frac{1}{0,2}\times \left( {{\operatorname{e}}^{0,2\times t}}-{{e}^{0,2\times 0}} \right)\)
Donc \({{V}_{f}}=0,05\times \frac{1}{0,2}\times \left( {{e}^{0,2\times 24}}-1 \right)+25\)
\(\Rightarrow\) Vf=50,12 L