Bilan sur une cuve agitée
Une cuve parfaitement agitée contient une concentration C d’un soluté donné. On l’alimente avec une solution concentrée du même soluté (Concentration d’entrée Ce) à un débit volumique Q. Le débit de sortie est égal à celui d’entrée, de manière à ce que le volume dans la cuve reste constant.
t0=0
On suppose que la concentration initiale dans la cuve est C0=Cs0=0.
Q: débit en m3/h
C: concentration en kg/m3
Question
Comment évolue la concentration C dans le réacteur au cours du temps?
Indice
Ecrire le bilan matière sur le soluté dans le système {cuve parfaitement agitée}.
Indice
Votre bilan se simplifie grâce à deux éléments :
1- Il n'y a pas de réaction ;
2- Les débits volumiques d'entrée et de sortie sont égaux.
Solution
Partons du cas général :
Qe le débit volumique d'entrée (en m3/s) d'un soluté B dans la cuve.
Un débit Qs est soutiré en continu.
Ce = concentration du soluté dans la solution d'entrée.
C = concentration du soluté dans la cuve.
On va écrire:
Les entrées
Les sorties
La production ou destruction
L'accumulation
Tous les termes du bilan doivent être écrits dans la même unité.
Choisissons ici d'écrire le bilan sur le débit massique (kg/h) du soluté.
Entrée de soluté = Qe*Ce
Sortie de soluté = Qs*Cs= Qs*C (le réacteur étant parfaitement agité)
Accumulation : c'est la variation de la quantité de soluté dans la cuve au cours du temps = \(\frac{d\left( V\times {{C}} \right)}{dt}\)
Production ou destruction : Supposons que le soluté soit consommé dans la cuve par une réaction chimique d'ordre 1 avec une constante de réaction notée k. La variation de sa concentration dans la cuve au cours du temps s'écrit alors : \(\frac{d{{C}}}{dt}=-k\times {{C}}\). Ramenée en kg/h, cette entité devient : \(-k\times V\times {{C}}\)
Ainsi le bilan matière global sur la cuve fonctionnant en continue s'écrit :
\(\frac{d\left( V\times {{C}} \right)}{dt}={{Q}_{e}}\times {{C}_{e}}-{{Q}_{s}}\times {{C}}-k\times V\times {{C}}\)
Dans le présent cas particulier :
Si le débit d'entrée et le débit de sortie sont égaux : Qe = Qs = Q alors :
\(\frac{d\left( V\times {{C}} \right)}{dt}=Q\times \left( {{C}_{e}}-{{C}} \right)-k\times V\times {{C}}\)
Si les débit sont égaux, alors il n'y a pas de variation du volume réactionnel dans la cuve. Dans ce cas l'équation devient : \(V\times \frac{d{{C}}}{dt}=Q\times \left( {{C}_{e}}-{{C}} \right)-k\times V\times {{C}}\)
Si en plus, il n'y a pas de réaction (la cuve est alors un simple mélangeur ou un échangeur thermique) : k = 0, alors :
\(V\times \frac{d{{C}}}{dt}=Q\times \left( {{C}_{e}}-{{C}} \right)\)
→ \(\frac{d{{C}}}{dt}=\frac{Q}{V}\times \left( {{C}_{e}}-{{C}} \right)\)
La solution de cette dernière équation donne la courbe C=f(t) qui représente finalement l'évolution de la concentration d'un traceur dans une cuve pour évaluer le temps de mélange.
Cette équation est réarrangée comme suit : \(\frac{Q}{V}dt=\frac{dC}{(C_e-C)}\)
Cette équation différentielle doit maintenant être intégrée afin d'obtenir l'expression de C en fonction du temps :
\(\int_{t=0}^{t}\frac{Q}{V}dt=\int_{C=0}^{C}\frac{dC}{(C_e-C)}\)
Ce qui donne : \(\frac{Q}{V}t=[-ln(C_e-C)]_{0}^{C}\)
Soit : \(\frac{Q}{V}t=-ln(C_e-C)+lnC_e donc \frac{Q}{V}t=ln\frac{Ce}{C_e-C}\)
Donc \(e^{\frac{Q}{V}t}=\frac{Ce}{C_e-C}\)
Il suffit maintenant de réarranger l'équation pour exprimer C en fonction de t :
\((C_e-C)\times e^{\frac{Q}{V}t}=C_e donc C_e\times (e^{\frac{Q}{V}t}-1)=C\times e^{\frac{Q}{V}t}\)
D'où : \(C=C_e\times (1-e^{-\frac{Q}{V}t})\)
Si on trace cette courbe (qualitativement, c'est-à-dire sans nécessairement assigner de valeurs aux constantes), on obtient l'allure suivante, qui montre une augmentation asymptotique
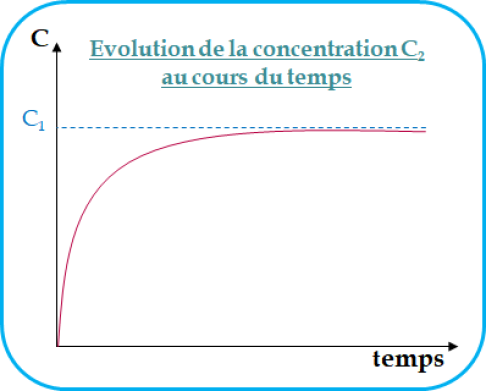
Question
Quel est le temps nécessaire pour obtenir Cs=0,99*Ce?
Solution
Cs=0,99*Ce revient à : \(\frac{C}{C_e}=0,99=(1-e^{-\frac{Q}{V}t})\)
Donc \(e^{-\frac{Q}{V}t}=0,01\) donc \(-\frac{Q}{V}\times t = ln0,01\)
Donc \(t=-\frac{V}{Q}\times ln0,01\)
Donc \(t=4,6\times t_s\) où ts est le temps de passage ou le temps de séjour moyen du soluté dans la cuve.