Transferts de matière dans les bioréacteurs

La diffusion moléculaire est une phénomène de transfert qui consiste en un mouvement des composés moléculaires d'un milieu 1 vers un milieu 2 sous l'action du gradient de potentiel chimique des composés entre les deux milieux. Le gradient de potentiel peut être approximé - sous certaines conditions - au gradient de concentration (figure ci-dessous).

Si le gradient est maintenu en alimentant le milieu concentré en composés et en les retirant du milieu peu concentré, la diffusion est continue. Cette situation correspond à celle d'un fermenteur où l'oxygène, apporté en continu, est également consommé en continu par les cellules mises en culture.

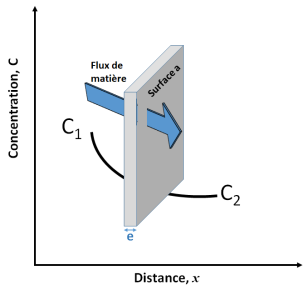
La densité de flux de composé diffusant à travers la surface A est décrit par la loi de Fick :

\(j=-D\times \frac{\partial c}{\partial x} =\frac{J} {a}\) 1^e Loi de FICK (1855)

où :

j = densité de flux, exprimée en kg.m^-2.s^-1

D = Coefficient de diffusion ou (diffusivité) exprimé en m².s^-1

C₁ et C₂ = concentrations en kg.m^-3

J = vitesse de transfert exprimé en kg.s^-1

a = surface d'échange exprimée en m²

L'équation précédente montre que la vitesse de transfert peut être améliorée en augmentant la surface d'échange entre les deux milieux, le gradient de concentration, le coefficient de transfert, ou alors en diminuant l'épaisseur du film.

Pour exemple : le coefficient de diffusion de l'oxygène dans l'eau à 25 °C et à pression atmosphérique est de 2,5*10^-9 m².s^-1.

Le mélange de fluide est très communément utilisé dans les procédés industriels pour accélérer l'homogénéisation des milieux réactionnels. Cependant, dans plusieurs cas, la diffusion moléculaire reste limitante :

- échelle de mélange : la turbulence dans le fluide permet le mélange par convection des solutions à différentes échelles allant jusqu'à l'échelle du plus petit tourbillon, dont la taille dépend des propriétés physico-chimique du milieu. En-dessous de cette échelle, l'homogénéisation se fait par diffusion moléculaire.

- réactions en phase solide : Quand des films, des flocs ou des champignons filamenteux ou des enzymes immobilisées sont mis en jeu dans un bio-procédé, le transfert de matière de l'interface vers le biocatalyseur est assuré par diffusion moléculaire à l'intérieur du milieu solide.

- transfert de matière entre phases : il s'agit typiquement du transfert d'oxygène d'une bulle de gaz vers le milieu de culture liquide. Quand deux phases sont en contact, la vitesse de fluide à l'interface s'en trouve significativement diminuée et la diffusion devient déterminante dans le transfert de matière.

La théorie du double film est un modèle simplificateur utile pour l'étude du transfert de matière entre deux phases.

Le transfert de matière d'une phase à une autre implique le transport des solutés de la première phase vers l'interface puis son transfert vers la seconde phase. La théorie du film consiste à imaginer qu'une fine pellicule de fluide (appelée couche limite) se forme dès que deux phases sont en contact.

Soit deux fluides non miscibles contenant un soluté A en concentrations différentes. Chacune des deux phases est considérée comme parfaitement mélangée. La concentration de A dans la première phase est notée C_A1 et celle dans la deuxième phase C_A2.

Selon la théorie du film, la turbulence de l'écoulement dans chaque phase s'annule à l'interface. Un film fin de fluide stagnant se forme de part et d'autre de l'interface. Le transfert de matière dans ces films fins se fait exclusivement par diffusion moléculaire. Les concentrations de part et d'autre de l'interface à l'intérieur de ces films changent selon le schéma ci-dessous :

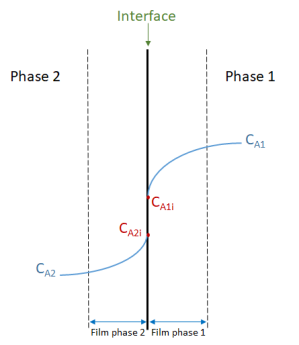
La différence de concentration entre les deux interfaces (C_A1i et C_A2i) provient de la possible différence d'affinité de A pour la phase 1 et la phase 2. A l'équilibre, le rapport entre ces deux concentrations donne un coefficient de partage entre les deux phases.

Le transfert de matière convectif a lieu lorsqu'un fluide est en mouvement. Dans ces cas, le transfert global de matière est nettement amélioré en comparaison avec les situations où seule la diffusion existe. Ainsi, lorsque deux milieux non miscibles sont en contact, les deux modes de transfert peuvent coexister et il peut s'avérer utile de les décrire dans leur globalité.

D'une manière générale, le transfert s'écrit :

vitesse de transfert α surface d'échange x force motrice

Le coefficient de proportionnalité étant le coefficient de transfert de matière entre les deux milieux.

La force motrice pour le transfert d'un composé A d'une première phase vers la deuxième peut être décrit comme étant le gradient de concentration de part et d'autre de l'interface. La vitesse de transfert du composé A du premier milieu fluide vers l'interface à travers la première couche limite s'écrit :

\(J=k\times a\times (C_{A1}-C_{A1i})\)

où a est l'aire interfaciale en m².m^-3

et k le coefficient de transfert de matière en m.s^-1

Cette équation montre que l'augmentation de l'aire interfaciale permet d'augmenter la vitesse de transfert du composé A.

On appelle résistance au transfert l'entité \(R_m=\frac{1}{k\times a}\)

L'interprétation du coefficient k est complexe dans la mesure où il englobe tous les phénomènes de transfert à l'interface, diffusifs et convectifs, avec l'influence de la couche limite. Il peut néanmoins être déterminé expérimentalement ou déterminés à partir de corrélations semi-empiriques.

Dans le cas des bioprocédés, les phases en contact peuvent être diverses :

• solide - liquide ;

• liquide - liquide entre phases non miscibles ;

• liquide - gaz.

Dans ce qui suit, nous allons détailler le cas du transfert gaz-liquide pour l'oxygénation des milieux de culture dans le cas des cultures aérobies.

Pour reprendre le mécanisme décrit plus haut et l'appliquer au cas du transfert gaz-liquide de l'oxygène en bioréacteur, le schéma de transfert se décline comme suit :

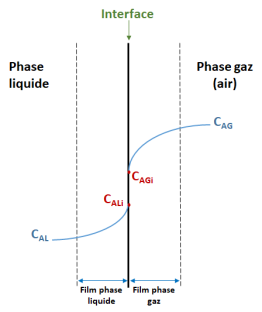
Où :

C_AG est la concentration de A dans la phase gaz ;

C_AL est la concentration de A dans la phase liquide ;

C_i est la concentration à l'interface.

Le transfert de matière à travers le film gazeux jusqu'à l'interface s'écrit :

\(J_{AG}=k_G\times a\times (C_{AG}-C_{AGi})\)

Le transfert de matière depuis l'interface à travers le film liquide s'écrit :

\(J_{AL}=k_L\times a\times (C_{AL}-C_{ALi})\)

où k_G et k_L sont les coefficients de transfert à travers le film gazeux et le film liquide respectivement.

C_ALi et C_AGi sont inaccessibles expérimentalement. Cependant, l'équilibre de partage entre les deux phases peut être connu et on peut écrire :

\(C_{AGi}=m \times C_{ALi}\)

avec : m le coefficient de partage du gaz A entre la phase gazeuse et la phase liquide.

Dans des conditions de transfert en régime permanent, on peut établir que : (J_AL = J_AG = J_A).

C_ALi et C_AGi étant inaccessibles expérimentalement, l'écriture d'un bilan global présente un intérêt particulier puisqu'elle permet concrètement l'étude du transfert à l'interface.

Le flux de matière transféré peut alors s'écrire comme un flux global, en utilisant un coefficient global de transfert entre les deux phases et un gradient global de concentrations.

On définit le coefficient global de transfert de matière dans la phase liquide K_L tel que : \(\frac{1}{K_La}=\frac{1}{mk_Ga}+\frac{1}{k_La}\)

Le gradient global s'écrit entre la concentration mesurée dans la phase liquide et la concentration fictive obtenue si la phase liquide était en équilibre avec la phase gaz. Cette dernière s'écrit C_AL*.

La vitesse globale de transfert peut alors s'écrire :

\(J_A=K_La\times(C_{AL}^*-C_{AL})\)

Lorsque le composé A est faiblement soluble dans la phase liquide (cas de l'oxygène en milieu aqueux), la résistance au transfert de matière dans la phase liquide est dominant et celle dans la phase gazeuse peut être négligée. Dans ce cas, l'expression de la résistance globale au transfert : \(\frac{1}{K_La}=\frac{1}{mk_Ga}+\frac{1}{k_La}\) peut être simplifiée en : \(\frac{1}{K_La}=\frac{1}{k_La}\) et donc la vitesse globale de transfert s'écrit :

\(J_A=k_La\times(C_{AL}^*-C_{AL})\)

Dans le cas du transfert d'oxygène on obtient :

S'il est possible d'avoir des mesures fiables de [O₂] ainsi que des estimations de [O₂]*, il est quasi-impossible d'avoir une estimation précise de a. L'aire interfaciale des bulles d'air incorporée par barbotage dans le bioréacteur dépend de la qualité du diffuseur, de la vitesse d'agitation, du débit de gaz, de la composition du milieu de culture, de la température, etc. Le coefficient k_L est également affecté par ces paramètres. En conséquence, k_L et a sont souvent combinés et c'est un coefficient global k_La (en T^-1) qui est estimé.