Croissance des micro-organismes
Identification des phases de croissance
Lorsqu'un micro-organisme est mis en culture dans des conditions non restrictives, on observe une croissance (une augmentation du nombre de cellules vivantes au cours du temps) de l'allure suivante :
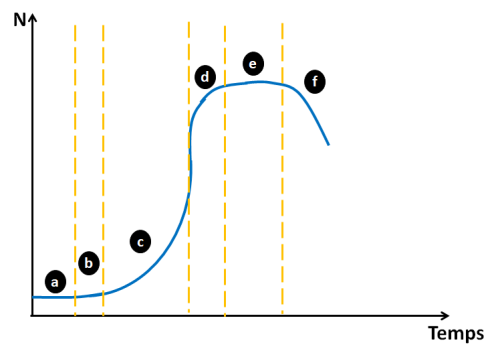
a - La phase de latence, avant le début des divisions cellulaires. Elle est souvent observée quand le micro-organisme doit s'adapter à un nouvel environnement de culture.
b - La phase d'accélération (pour certaines espèces cette phase n'est pas décelable)
c - La phase exponentielle, durant laquelle les cellules se divisent à vitesse constante et maximale.
d - La phase de décélération, lorsque les substrats commencent à devenir limitant et les métabolites primaires et secondaires commencent à s'accumuler fortement dans le milieu de culture.
e - La phase stationnaire, lorsque la vitesse de croissance et la vitesse de mortalité cellulaire se compensent.
f - La phase de dégénérescence des cellules (mort des cellules)
Ces phases ne sont pas reproductibles pour tous types de cellules vivantes. (Exemple des cellules de neurones, ou des cellules reproductrices, dont la multiplication suit des rythmes très particuliers).
Dans ce qui suit, nous parlerons essentiellement de la croissance des micro-organismes unicellulaires.
Temps de génération, taux de croissance et loi de Monod
Temps de génération
Le principe de croissance des cellules vivantes est assez simple : chaque cellule dédouble sa machinerie interne (mitochondries, réticulum, matériel génétique) et finit par se scinder en deux nouvelles cellules. Quand les cellules sont mises en culture dans des conditions favorables, avec un milieu de culture auquel elles sont déjà adaptées, elles se multiplient à un rythme constant, conformément au schéma ci-dessous :
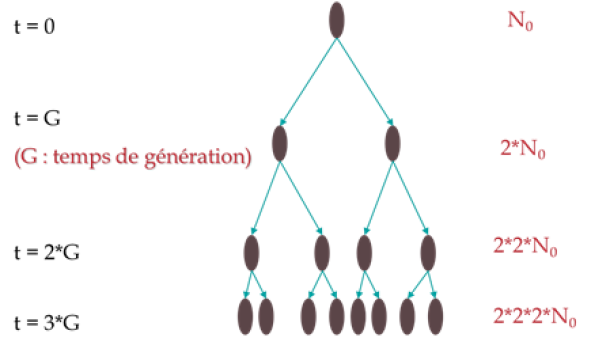
On définit donc un temps de génération constant, qui résulte en une croissance en puissance du nombre de cellules au cours du temps, selon l'équation suivante :
\(N={{N}_{0}}\times {{2}^{\frac{t}{G}}}\)
avec : \(\frac{t}{G}=n\text{ }\left( \text{nombre de g }\!\!\acute{\mathrm{e}}\!\!\text{ n }\!\!\acute{\mathrm{e}}\!\!\text{ rations} \right)\)
Exemples de temps de génération
Les temps de culture peuvent être extrêmement variables selon les cellules vivantes mises en culture et donc leur temps de dédoublement. Le tableau ci-dessous donne des estimations des temps de génération pour différentes cellules. Vous remarquerez que ces temps varient de 0,16h pour les bactéries les moins exigeantes à plus de 80h pour certaines cellules d'algues.
Micro-organisme | Température (°C) | Temps de génération (h) |
|---|---|---|
Bactéries | ||
Beneckea natriegens | 37 | 0.16 |
Escherichia coli | 40 | 0.35 |
Bacillus subtilis | 40 | 0.43 |
Pseudomonas aeruginosa | 37 | 0.58 |
Colstridium botulinum | 37 | 0.58 |
Mycobatcterium tuberculosis | 37 | 12 |
Treponema pallidum | 37 | 33 |
champignons | ||
Saccharomyces cerevisiae | 30 | 2 |
Monilinia fraa | 25 | 30 |
Algues | ||
Scenedesmas quadricauda | 25 | 5.9 |
Chlorella pyrenoidosa | 25 | 7.75 |
Euglena gracilis | 25 | 10.9 |
Ceratium tripos | 20 | 82.8 |
Cellules de mammifères | ||
cellules d'ovaires de hamster chinois (CHO) | 37 | 12-24 |
Taux de croissance, taux de croissance maximum
Les deux précédentes équations donnent : \(\text{N}={{\text{N}}_{0}}\times {{\text{e}}^{\text{t}\times \frac{\text{ln}2}{\text{G}}}}\)
En posant : \(\frac{\text{ln}2}{\text{G}}=\text{ }\!\!\mu\!\!\text{ }\) on appelle taux de croissance la grandeur µ, qui s'exprime en temps-1. On peut également la rencontrer sous le m'appellation de vitesse spécifique de croissance.
\(\text{N}={{\text{N}}_{0}}\times {{\text{e}}^{\text{ }\!\!\mu\!\!\text{ t}}}\) (solution analytique, par ailleurs, de l'équation différentielle du premier ordre \(\frac{dN}{dt}=\mu N\))
Pendant la phase exponentielle, le temps de génération est constant donc µ est constant et égal à sa valeur maximale notée µmax (c'est le taux de croissance maximum) →
\(\frac{dN}{dt}={{\mu }_{\max }}\times N\) |
|---|
Ce modèle s'écrit également sur la concentration \([X]\) de cellules dans le milieu réactionnel comme suit : \(\frac{d[X]}{dt}=\mu\times [X]\)
Après la phase exponentielle : La phase exponentielle dure tant que les cellules disposent de tous les nutriments dont elles ont besoin, et tant que des métabolites (produits de l'activité des cellules) inhibiteurs ne se sont pas accumulés dans le milieu. Dès que l'une de ces conditions n'est plus remplie, la croissance des cellules ne suit plus une phase exponentielle de croissance.
Loi de Monod et bilans matières
On observe alors les trois phénomènes cinétiques suivants :
1/ µ n'est plus constant et dépend de la concentration de substrat :
\(\mu =\frac{{{\mu }_{\max }}\times [S]}{{{K}_{S}}+[S]}\) |
|---|
où Ks : constante de saturation relative au substrat S (g de substrat/L)
2/ la variation globale du nombre de micro-organismes tient à la fois compte de la croissance et de la mortalité et s'écrit :
\(\frac{dN}{dt}=\frac{{{\mu }_{\max }}\times [S]}{{{K}_{S}}+[S]}\times N-k{}_{d}\times N\) |
|---|
Où kd : constante de mortalité (h-1)
3/ Et la variation de la concentration de substrat s'écrit :
\(\frac{d[S]}{dt}=-\frac{1}{Y_{X/S}}\times \frac{{{\mu }_{\max }}\times [S]}{{{K}_{S}}+[S]}\times N\) |
|---|
Où YX/S : masse de micro-organismes produits par masse de substrat consommé = rendement de croissance sur le substrat S.
\[\]
La loi de Monod ressemble beaucoup à l'équation de Michaelis-Menten, à la différence qu'elle est obtenue par une approche empirique alors que la première résulte d'un développement théorique.
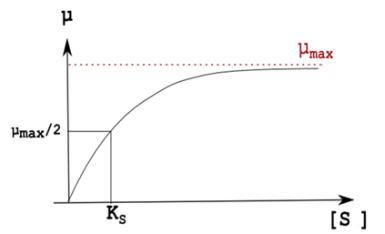
On peut tracer l'évolution de µ en fonction de la concentration de substrat et on retombe sur les mêmes raisonnements : KS est la concentration de substrat qui donne une valeur de µ égale à la moitié de µmax.
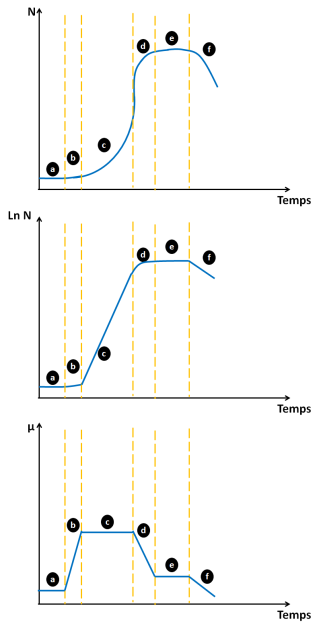
Complément : Courbe de croissance, courbe en échelle logarithmique et courbe de taux de croissance
La figure ci-dessous permet de visualiser l'évolution du nombre de cellules avec µ.
Tracer la troisième courbe \(\mu =f(t)\) permet d'identifier graphiquement la phase exponentielle de croissance et de déterminer \(\mu_{max}\).