Bioréacteurs discontinus [Conduite des bioréacteurs]

Bioréacteurs discontinus

Méthode : Préalable

Quel que soit le mode de fonctionnement d'un bioréacteur, afin de le caractériser correctement et d'être en mesure de simuler son fonctionnement, il faut écrire :

le bilan matière sur la biomasse ;
un bilan matière sur chaque substrat important : le principal substrat carboné, l'oxygène dissous si nécessaire, le CO₂ pour les organismes photosynthétiques, etc.
un bilan matière sur chaque produit important : produit(s) d'intérêt ou métabolite(s) secondaire(s) à effet notoire (par exemple inhibiteur) sur le procédé.

Le système d'équations obtenu n'est pas toujours aisé à résoudre analytiquement et le recours à des méthodes de résolution numériques peut être nécessaire.

Ecriture des bilans

\[\]Soit un fermenteur discontinu parfaitement agité. La concentration initiale de micro-organismes est notée [X]₀ et la concentration initiale de substrat [S]₀.

La vitesse spécifique de croissance du micro-organisme, µ, obéit à la loi de Monod :

\(\mu =\frac{{{\mu }_{\max }}\times \left[ S \right]}{{{K}_{S}}+\left[ S \right]}\)

La cinétique de croissance suivant une loi du premier ordre, la concentration de micro-organismes au cours du temps s'écrit :

\(\left[ X \right]=\left[ {{X}_{0}} \right]\times {{e}^{\mu \times t}}\)

Et la variation de la concentration de S au cours du temps est calculée grâce au rendement de conversion de substrat en biomasse :

\({{r'''}_{S}}=\frac{d\left[ S \right]}{dt}=-\frac{1}{{{Y}_{X/S}}}\frac{d\left[ X \right]}{dt}\)

donc \({{r'''}_{S}}=-\frac{1}{{{Y}_{X/S}}}\frac{{{\mu }_{\max }}\left[ S \right]}{{{K}_{s}}+\left[ S \right]}\left[ X \right]\)

avec :

K_S = la constante de demi-vitesse de consommation de S par les micro-organismes (mg/L)

Y_X/S = masse de micro-organismes produits par masse de substrat consommé.

Le taux de conversion du substrat à l'instant t est défini par \(\theta\) ou \(X\) selon les sources, comme suit : \(\theta =\frac{{{\left[ S \right]}_{0}}-\left[ S \right]}{{{\left[ S \right]}_{0}}}\)

*************************************

Prenons le cas le plus simple : celui où il n'y a pas de limitation de la croissance par la concentration de substrat. Dans ce cas la croissance se déroule en phase exponentielle etµ est constant à sa valeur maximale µ_max. Dans ce cas, il est possible de résoudre les équations bilans sur la biomasse, le substrat et le produit et d'en extraire l'expression du temps ou l'expression de la concentration de substrat, de biomasse ou de produit.

1- La résolution de l'équation d'expression de r'''_s ci-dessus permet de calculer le temps de réaction nécessaire pour atteindre un taux de conversion donné donc une concentration résiduelle de substrat [S] :

\(t=\frac{1}{{{\mu }_{\max }}}\times \ln \left( 1+\frac{{{Y}_{X/S}}\times \left( \left[ {{S}_{0}} \right]-\left[ S \right] \right)}{\left[ {{X}}\right]_{0}} \right)\)

Cette expression de t correspond au cas le plus simple (purement fictif) c'est-à-dire le cas où il n'y a pas de consommation de substrat due à la maintenance, ni de production de métabolite.

2- Lorsqu'une consommation de substrat due à la maintenance est présente, soit dans la plupart des cas, l'expression de r_s est modifiée et le temps de réaction nécessaire devient :

\(t=\frac{1}{{{\mu }_{\max }}}\times \ln \left( 1+\frac{\left( \left[ {{S}_{0}} \right]-\left[ S \right] \right)}{\left( \frac{1}{{{Y}_{X/S}}}+\frac{{{m}_{s}}}{{{\mu }_{\max }}} \right)\times \left[ {{X}} \right]_{0}} \right)\)

3- Enfin, le temps de réaction peut être calculé en fonction de la concentration de produit souhaitée comme résultat, donc sur la base d'un bilan matière sur le produit. Cela donne l'expression ci-dessous :

\(t=\frac{1}{{{\mu }_{\max }}}\times \ln \left( 1+\frac{{{\mu }_{\max }}}{{{\left[ X \right]}_{0}}{{q}_{p}}}\left( {{\left[ P \right]}_{f}}-{{\left[ P \right]}_{0}} \right) \right)\)

où : q_p = vitesse spécifique de production de P (h^-1)

Vous pouvez vous-mêmes démontrer ces trois dernières expressions de t.

Méthode :

La vidéo ci-dessous présente la démonstration qui conduit à la caractérisation des 3 profils : X=f(t), S=f(t) et P=f(t).

Démonstration des profils de concentration en batch

Les profils cinétiques qui découlent de ces modèles sont représentés sur le graphique ci-dessous :

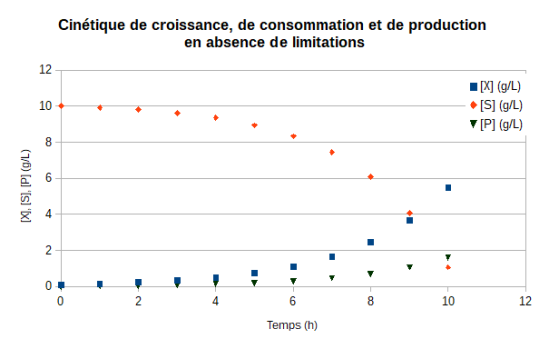
Exemples d'allures des cinétiques batch sans limitations

Remarque :

En cas de limitation de substrat, la croissance ne se déroule plus en phase exponentielle. µ n'est plus à sa valeur µ_max mais varie en fonction de S (loi de Monod) et il n'est pas possible de résoudre analytiquement les équations de bilan matière.

Ci-dessous les profils cinétiques possibles :

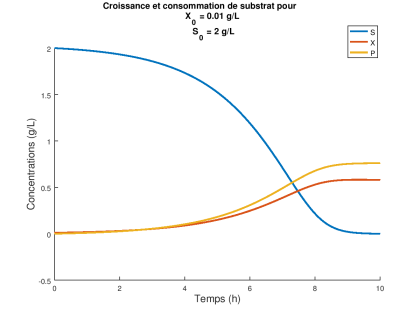
Complément : Etude des performances d'un bioréacteur discontinu

Pour le calcul des performances d'un batch, tous les temps dits "morts" doivent être pris en compte, c'est à dire les temps de fonctionnement pendant lesquels il n'y a pas de production de biomasse ou de produit d'intérêt.

Ces temps morts correspondent au temps de préparation du fermenteur, au temps de latence en début de fermentation, au temps de vidange du fermenteur, etc.

Le paramètre commun de calcul de la performance d'une fermentation batch est la Productivité. Elle se définit comme étant la concentration de cellules produite par unité de temps :

Productivité cellulaire d'un batch
\(P=\frac{\Delta X}{\Delta t}\)

Si l'ensemble des temps morts est pris en compte, la productivité s'écrit :

\(P=\frac{\Delta X}{temp{{s}_{morts}}+\left( \frac{1}{{{\mu }_{max}}}\ln \frac{X}{{{X}_{0}}} \right)}\)

On voit que contrairement à la productivité globale, la productivité instantanée est variable au cours du temps et atteint son maximum pendant la phase exponentielle. Ainsi, si nous superposons la courbe de croissance des cellules avec la courbe de productivité, le graphique suivant est obtenu :

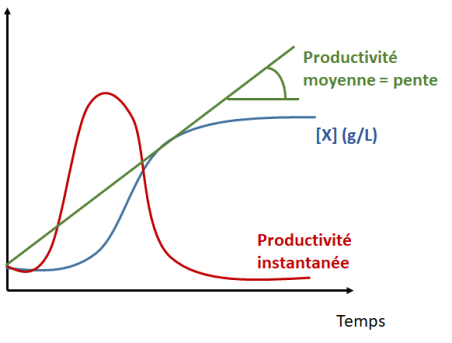
Productivité moyenne et productivité instantanée d'un batch

La vidéo ci-dessous redonne la démonstration des calculs de productivité (instantanée, globale, maximale) dans un batch et leur signification :

Productivité d'un Batch